Cascade Control Systems Design - Tunings

Procedure for Cascade Control Systems Design:
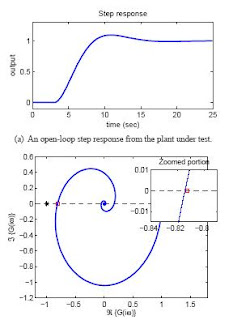
Choice of Suitable PID TuningsAbstract: This paper provides an approach for the application of PID controllers
within a cascade control system configuration. Based on considerations about the
expected operating modes of both controllers, the tuning of both inner and outer loop
controllers are selected accordingly. This fact motivates the use of a tuning that,
for the secondary controller, provides a balanced set-point / load-disturbance performance.
A new approach is also provided for the assimilation of the inner closed-loop
transfer function to a suitable form for tuning of the outer controller. Due to the fact
that this inevitably introduces unmodelled dynamics into the design of the primary
controller, a robust tuning is needed.

2 Cascade Control


3 g-tuning for balanced Servo/Regulation
4 Approach for Cascade Control Design
4.1 Inner loop and outer loop process models
4.2 Inner loop controller tuning
Set-point tuning settings
Load-disturbance tuning settings
4.3 Model for Outer loop tuning
4.4 Outer loop controller tuning
5 Equivalent model approximation
6 Example
7 Conclusions
http://www.journal.univagora.ro/download/pdf/134.pdf

How to Tune Cascade Loops
1 An overview of Cascade Control.
What's The Inner Loop For?
• Reduces phase lag of inner process
• Disturbances to the inner loop are
compensated for before they upset the
outer loop
• Prevents non-linearities in the inner loop
from reaching the outer loop

2 Tuning Cascade Control Loops.
What happens when cascade loops
are poorly tuned?
• Loops “fight” each other
• Create oscillations
• Neither variable is properly controlled
• Operator puts loop in manual.
Tuning Cascade Loops
1. Always check for measurement and
valve-related issues.
2. Inner Loop Tuning - put slave into
Local Auto or Manual and tune the
slave controller as a normal PID loop.
3. Outer Loop Tuning - put slave into
Cascade and tune master controller
as a normal PID loop.
4. Adjust outer loop tuning values to
ensure that the RRT (Relative
Response Time) of outer loop is 3-5
times slower than the inner loop.

3 Case Study.

http://www.expertune.com/articles/UG2007/CascadeTuning.pdf

Cascade Control
Handle Processes that Challenge Regular PID Control

In previous columns we have named lags in a process as major obstacles to good temperature control. When they are inconveniently long and come in multiple stages, first try to determine where changes to process design can avoid or reduce lags. Then do your best with PID control and if you fail to obtain the response you hoped for you can turn to cascade control.



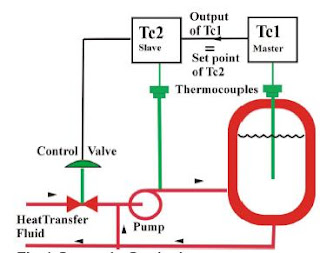
Tuning.Tune the slave loop first. Set TC1 to manual. Remove integral and derivative action from TC2 and tune it aiming for tight control. Absence of derivative avoids excessive activity of the slave loop. Overall integral action to remove offset in the vessel temperature is already provided by the master controller.

When tuning the master loop, return to cascade control, remove derivative action and tune in the normal way. Note that the slave loop now becomes part of the master loop that you are tuning at TC1. Bumpless transfer between auto, manual and cascade will be a standard feature of TC1.
Set point limits on the slave loop. If you know the range of TC2 (fluid) temperatures needed to hold the vessel temperature under all expected conditions, put those values as limits on the set point of TC2.

http://www.pacontrol.com/download/Cascade%20Control%20-%20Handle%20Processes%20that%20Challenge%20Regular%20PID%20Control.pdf


Cascade Controller - Auto Tuning

Relay Auto Tuning Of Parallel Cascade Controller
Abstract
The present work is concerned with relay auto tuning of
parallel cascade controllers. The method proposed by
Srinivasan and Chidambaram [10] to analyze the conventional
on-off relay oscillations for a single loop feedback controller is
extended to the relay tuning of parallel cascade controllers.
Using the ultimate gain and ultimate cross over frequency of
the two loops, the inner loop (PI) and outer loop (PID)
controllers are designed by Ziegler-Nichols tuning method. The
performances of the controllers are compared with the results
based on conventional relay analysis. The improved method of
analyzing biased auto tune method proposed for single
feedback controller by Srinivasan and Chidambaram [11] is
also applied to relay auto tune of parallel cascade controllers.
The proposed methods give an improved performance over that
of the conventional on-off relay tune method.

http://www.iaeng.org/publication/WCECS2007/WCECS2007_pp158-162.pdf

PID Controllers Auto Tuning - Relay Feedback

Relay Feedback Auto Tuning of PID Controllers

IntroductionFor a certain class of process plants, the so-called \auto tuning" procedure
for the automatic tuning of PID controllers can be used. Such a procedure
is based on the idea of using an on/off controller (called a relay controller)
whose dynamic behaviour resembles to that shown in Figure 1(a). Starting
from its nominal bias value (denoted as 0 in the Figure) the control action
is increased by an amount denoted by h and later on decreased until a value
denoted by -h.




The closed-loop response of the plant, subject to the above described ac-
tions of the relay controller, will be similar to that depicted in Figure 1(b).
Initially, the plant oscillates without a de¯nite pattern around the nominal
output value (denoted as 0 in the Figure) until a de¯nite and repeated out-
put response can be easily identi¯ed. When we reach this closed-loop plant
response pattern the oscillation period (Pu) and the amplitude (A) of the
plant response can be measured and used for PID controller tuning. In fact,
the ultimate gain can be computed as:
Having determined the ultimate gain Kcu and the oscillation period Pu
the PID controller tuning parameters can be obtained from the following
table:
Example of Relay Feedback Auto Tuning of PID Controllers

http://200.13.98.241/~antonio/cursos/control/notas/siso/atv.pdf
Relay-based PID Tuning
ABSTRACT
Relay-based auto tuning is a simple way to tune PID controllers
that avoids trial and error, and minimises the possibility
of operating the plant close to the stability limit.

http://homepages.ihug.co.nz/~deblight/AUTResearch/papers/relay_autot.pdf


An Improved Relay Auto Tuning of PID Controllers for SOPTD
Systems


Difficulties of loop tuning
When you discuss loop tuning with instrument and control
engineers, conversation soon turns to the Zeigler-Nichols
(ZN) ultimate oscillation method. Invariably the plant engineer
soon responds with ‘Oh yes, I remember the ZN tuning
scheme, we tried that and the plant oscillated itself into
oblivion — bad strategy. Moreover when it did work, the
responses are overly oscillatory’
So given the tedious and possibly dangerous plant trials
that result in poorly damped responses, it behoves one to
speculate why it is often the only tuning scheme many instrument
engineers are familiar with, or indeed ask if it has
any concrete redeeming features at all.
In fact the ZN tuning scheme, where the controller gain
is experimentally determined to just bring the plant to the
brink of instability is a form of model identification. All
tuning schemes contain a model identification component,
but the more popular ones just streamline and disguise that
part better. The entire tedious procedure of trial and error
is simply to establish the value of the gain that introduces
half a cycle delay when operating under feedback. This is
known as the ultimate gain Ku and is related to the point
where the Nyquist curve of the plant in Fig. 1(b) first cuts
the real axis.

The problem is of course, is that we rarely have the luxury
of the Nyquist curve on the factory floor, hence the
experimentation required.
Abstract Using a single symmetric relay
feedback test, a method is proposed to identify
all the three parameters of a stable second order
plus time delay (SOPTD) model with equal time
constants. The conventional analysis of relay
auto-tune method gives 27% error in the
calculation of ku,. In the present work, a method
is proposed to explain the error in the ku
calculation by incorporating the higher order
harmonics. Three simulation examples are given.
The estimated model parameters are compared
with that of Li et al. [4] method and that of
Thyagarajan and Yu [8] method. The open loop
performance of the identified model is compared
with that of the actual system. The proposed
method gives performances close to that of the
actual system. Simulation results are also given
for a nonlinear bioreactor system. The open loop
performance of the model identified by the
proposed method gives a performance close to
that of the actual system and that of the locally
linearized model. SOPTD model, symmetric relay, auto-tuning

http://ntur.lib.ntu.edu.tw/bitstream/246246/87370/1/09.pdf

DEVELOPMENT OF AN AUTO-TUNING PID AND
APPLICATIONS TO THE PULP AND PAPER INDUSTRY
Abstract
An auto-tuning industrial PID is presented. The autotuning
is realized in three steps. The process is first
adequately excited in order to generate good quality data
for the second step, the process identification. The last step
is the PID tuning based on the evaluated parametric model.
The auto-tuning PID has been implemented on two
different control systems and successful applications to
processes of the pulp and paper industry are analyzed.

http://www.iaeng.org/publication/WCECS2007/WCECS2007_pp175-181.pdf

Auto-tune system using single-run relay feedback test
and model-based controller design
Abstract
In this paper, a systematic approach for auto-tune of PI/PID
controller is proposed. A single run of the relay feedback experiment
is carried out to characterize the dynamics including the type
of damping behavior, the ultimate gain, and ultimate frequency.
Then, according to the estimated damping behavior, the process
is classified into two groups. For each group of processes,
modelbased rules for controller tuning are derived in terms of
ultimate gains and ultimate frequencies. To classify the processes,
the estimation of an apparent deadtime is required. Two artificial
neural networks (ANNs) that characterize this apparent deadtime using
the ATV data are thus included to facilitate this estimation of
this apparent deadtime. The model-based design for this auto-tuning
makes uses of parametric models of FOPDT (i.e. first-order-plus-dead-time)
and of SOPDT (i.e. second-order-plus-dead-time)
dynamics. The results from simulations show that the controllers
thus tuned have satisfactory results compared with those from
other methods.

Tuning strategy for the model-based auto-tune system.


http://w3.gel.ulaval.ca/~desbiens/publications/DevelopmentOfAnAutoTuningPID.pdf

MODIFICATION AND APPLICATION OF AUTOTUNING
PID CONTROLLER
Abstract. This contribution presents a modified autotuning algorithm of the PID controller.
The motivation for the modification of the basic autotuning algorithm is to enlarge the class
of processes to which it can be applied. The basic autotuning algorithm introduced by
Åstrom and Hägglund is extended by the preliminary identification procedure and through
the usage of the dead time compensating controller. These modifications are detailed
through the description of the algorithms’ functioning. The proposed algorithm has been
implemented in the programmable logic controller (PLC) Siemens SIMATIC S7-300. The
experimental results confirm the good robustness properties of the proposed algorithm,
which were demonstrated in a simulation study.

Structure of the modified autotuning PID controller.


http://act.rasip.fer.hr/old/papers/MED00_062.PDF