AUTO-TUNING CONTROL SYSTEM

DESIGN AND EVALUATION OF AN AUTO-TUNING CONTROL SYSTEM
FOR AN ALTITUDE TEST FACILITY
Abstract
Simulated altitude testing of large aircraft engines is a
very expensive, but essential step in the development and
certification of gas turbines used by commercial airlines. A
significant contributor to the cost of this process is the
time-intensive task of manually tuning the facility control
system that regulates the simulated flight condition. Moreover,
control system tuning must be performed each time
the test conductor changes the flight condition. An adaptive
control system that automatically performs this task can
significantly reduce the costs associated with this type of
engine testing.

This paper examines the features of an auto-tuning
controller architecture that contains both disturbance feedforward
and PID feedback components in a two-input, twooutput
multivariable configuration. The paper reviews the
underlying concepts of an auto-tuning system and contrasts
its advantages/disadvantages with respect to other adaptive
control techniques. The algorithm used to automatically
tune the controller does not require a facility model. However,
a nonlinear facility model was developed and used to
substantiate a decoupled-loop design approach, to validate
the controller design concept, and to evaluate the resulting
adaptive control system design performance. This analysis
and other practical design issues that impact the auto-tuning
control system performance are addressed in the paper. The
paper also presents results that illustrate the automatic tuning
sequence and the disturbance rejection performance
exhibited by this system during large engine transients at
several key points in the flight envelope. The auto-tuning
controller described in the paper was implemented at a
Pratt & Whitney flight test facility used in the development
of large, high bypass ratio gas turbines.

Rationale for the Auto Tune Control Concept
Unlike the MRAC and STR concepts, the Auto-Tune adjustment
(adaptation) mechanism does not require any a
priori information about system dynamics to compute the
PID controller parameters. Moreover, an Auto-Tune system
only updates the controller on an operator-demand basis.
The MRAC and STR methods do not explicitly interact
with the system operator. These two characteristics of the
auto-tuning concept were the primary factors in selecting
this adaptive concept for the altitude test facility application.
This section examines the underlying features of the
Auto-Tune concept and motivates the rationale for selecting
a PID controller for this application.

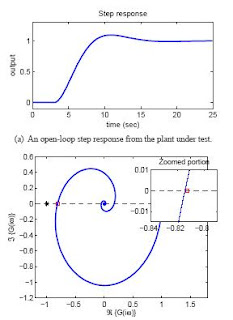
The automatic tuning performed with this scheme can be
characterized as a crude, but robust method that identifies
two key parameters characterizing process dynamics. The
Auto-Tune adaptation algorithm approaches the control
design in a manner quite familiar to first-generation single
input/single output control system designers. The fundamental
idea centers on determining the gain and frequency
at which the system dynamics become conditionally stable
under pure proportional feedback control. These frequencydomain
characteristics of the system are designated as the
ultimate gain and ultimate frequency, respectively. Using
Ziegler-Nichols relationships, the PID controller parameters
can be determined from the ultimate gain and frequency
information. It is well known that PID control systems
designed with the Ziegler-Nichols method exhibit
very good disturbance rejection performance, but tend to
have significant overshoot when responding to set-point
changes (Astrom & Hagglund - 1995). Degraded set point
responses do not present a problem in the altitude test facility
application since the control problem focuses completely
on disturbance rejection performance. The chamber
pressure and plenum pressure set points remain at fixed
values throughout an engine transient test scenario.

As in most control system synthesis problems, both time
and frequency based methods exist for formulating an experiment
that produces the information required to compute
the Ziegler-Nichols gains. In most practical control applications,
a frequency-based experiment produces superior results
and was the method chosen in this application. The
central idea in the frequency-based approach relies on the
fact that most real systems produce stable limit-cycles under
relay feedback. The theoretical basis for this statement
was developed in Astrom - 1991. The method of harmonic
balance or describing function method (Gelb and VanderVelde
– 1968) provides the mathematical framework for
analyzing relay-induced limit-cycles and extracting the
ultimate gain and ultimate frequency from the experimental
data.

http://web.iac-online.com/images/Publications/35.pdf
On-line PID Controller Design via a Single Auto-tuning Neuron

Abstract:
A simple tuning strategy for PID controller design will be proposed in this paper. With the
use of single neural estimator (SNE), three control gains of PID controller are not fixed during the
control procedure, but will be adjusted on-line such that better output response can be achieved. In
this control strategy the exact model of plant will not need to be known and identified. Lastly, two
simulation results are provided to show the control performance by using the proposed adaptive PID controller.

1. Introduction
2. Preliminaries
2.1 Auto-tuning neuron
2.2 PID controller
3. Self-tuning Adaptive PID
Controller
3.1 MIT rule
3.2 Control structure and algorithm
3.2.1 A tuning algorithm for PID control gains
3.2.2 A tuning algorithm for the SNE
4. Illustrative Examples
5. Conclusions

http://www.kyu.edu.tw/93/95paper/v8/95-061.pdf

Auto-Tuning of PID Controllers via Extremum Seeking
Abstract—The proportional-integral-derivative (PID) controller
is widely used in the process industry, but to various
degrees of effectiveness because it is sometimes poorly tuned.
The goal of this work is to present a method using extremum
seeking (ES) to tune the PID parameters such that optimal
performance is achieved. ES is a non-model based method
which searches on-line for the parameters which minimize a
cost function; in this case the cost function is representative
of the controllers performance. Furthermore, this method has
the advantage that it can be applied to plants in which
there is no knowledge of the model. We demonstrate the
ES tuning method on a cross section of plants typical of
those found in industrial applications. The PID parameters
are tuned based on the results of step response simulations to
produce a response with minimal settling time and overshoot.
Additionally, we have compared these results to those found
using other tuning methods widely used in industry.

Overall ES PID tuning scheme.





http://www.nt.ntnu.no/users/skoge/prost/proceedings/acc05/PDFs/Papers/0401_ThA17_2.pdf

Auto-Tuning Control Base on Ziegler-Nichols

Auto-Tuning Control Using Ziegler-Nichols
Automatic step testsOne of the earliest auto-tuning controllers still on the market is the 53MC5000 Process Control Station from MicroMod Automation. It uses the Easy-Tune algorithm originally developed at Fischer & Porter (now part of ABB) in the early 1980s. It automatically executes a step test similar to the open-loop Ziegler-Nichols method that forces the controller to make an abrupt change in its control effort while sensor feedback is disabled.

The amount by which the process variable subsequently changes and the time required
for it to reach 63.2% of its final value indicate the steady-state gain and time constant of the process, respectively. If the sensor in the loop happens to be located some distance from the actuator, the process’s response to such a step input may also demonstrate a deadtime between the instant that the step was applied and the instant that the process variable first began to react.

These three model parameters tell the Easy- Tune algorithm everything it needs to know about the behavior of a typical process, allowing it to predict how the process will react to any corrective effort, not just step inputs. That in
turn allows the Easy-Tune algorithm to compute tuning parameters to make the controller compatible with the process.



Closed loop tests
In 1984, Karl Åström and Tore Hägglund of the Lund (Sweden) Institute of Technology
published an improved version of Ziegler and Nichols’ closed-loop tuning method. Like the open-loop method, this technique excites the process to identify its behavior, but without disabling sensor feedback.

The Åström-Hägglund method works by forcing the process variable into a series of
sustained oscillations known as a limit cycle. The controller first applies a step input to the process and holds it at a user-defined value until the process variable passes the setpoint. It then applies a negative step and waits for the process variable to drop back below the setpoint. Repeating this procedure each time the process variable passes the setpoint in either direction forces the process variable to oscillate out of sync with the control effort, but at the same frequency. See the “Relay Test” graphic. The time required to complete a single oscillation is known as the process’s ultimate period (Tu), and the relative amplitude of the two oscillations multiplied by 4/π gives the ultimate gain (Pu). Ziegler and Nichols theorized that these two parameters could be used instead of the steady-state gain, time constant, and deadtime to compute suitable tuning parameters according to their famous tuning equations or tuning rules shown in the equation on the left.

They discovered empirically that these rules generally yield a controller that responds quickly to intentional changes in the setpoint as well as to random disturbances to the process variable. However, a controller thus tuned will also tend to cause overshoot and oscillations in the process variable, so most auto-tuning controllers offer several sets of alternative tuning rules that make the controller less aggressive to varying degrees. An operator typically only has to select the required speed of response (slow, medium, fast), and the controller chooses appropriate rules automatically.

http://www.das.ufsc.br/~aarc/ensino/posgraduacao/DAS6613/Auto-Tuning%20Control%20Using%20Ziegler-Nichols.pdf
REVISITING THE ZIEGLER-NICHOLS TUNING RULES
FOR PI CONTROL — PART II
THE FREQUENCY RESPONSE METHOD
ABSTRACT
This paper presents an analysis of the Ziegler-Nichols frequency response
method for tuning PI controllers, showing that this method has severe
limitations. The limitations can be overcome by a simple modification for
processes where the time delay is not too short. By a major modification it is
possible to obtain new tuning rules that also cover processes that are lag
dominated.

I. INTRODUCTION
II. TEST BATCH AND DESIGN METHOD
2.1 The MIGO design method
2.2 The test batch
2.3 The AMIGOs tuning rules
2.4 Parameterization
III. A FIRST ATTEMPT
3.1 Stable processes
3.2 Integrating processes
3.3 Tuning rules for balanced and
delay-dominated processes
3.4 Summary
IV. ANALYSIS
4.1 Modified tuning procedures
V. THE AMIGOF TUNING RULES
5.1 Other values of Ms
5.2 How to find the frequency ωφ?
5.3 Summary
VI. AN INTERPRETATION OF
THE RESULTS
VII. EXAMPLES
Example 1. LAG DOMINATED DYNAMICS
Example 2. BALANCED LAG AND DELAY
Example 3. DELAY DOMINATED DYNAMICS
VIII. CONCLUSION

http://www.ajc.org.tw/pages/PAPER/6.4PD/AC0604-P469-FR0371.pdf

PID Controllers Auto Tuning - Relay Feedback

Relay Feedback Auto Tuning of PID Controllers

IntroductionFor a certain class of process plants, the so-called \auto tuning" procedure
for the automatic tuning of PID controllers can be used. Such a procedure
is based on the idea of using an on/off controller (called a relay controller)
whose dynamic behaviour resembles to that shown in Figure 1(a). Starting
from its nominal bias value (denoted as 0 in the Figure) the control action
is increased by an amount denoted by h and later on decreased until a value
denoted by -h.




The closed-loop response of the plant, subject to the above described ac-
tions of the relay controller, will be similar to that depicted in Figure 1(b).
Initially, the plant oscillates without a de¯nite pattern around the nominal
output value (denoted as 0 in the Figure) until a de¯nite and repeated out-
put response can be easily identi¯ed. When we reach this closed-loop plant
response pattern the oscillation period (Pu) and the amplitude (A) of the
plant response can be measured and used for PID controller tuning. In fact,
the ultimate gain can be computed as:
Having determined the ultimate gain Kcu and the oscillation period Pu
the PID controller tuning parameters can be obtained from the following
table:
Example of Relay Feedback Auto Tuning of PID Controllers

http://200.13.98.241/~antonio/cursos/control/notas/siso/atv.pdf
Relay-based PID Tuning
ABSTRACT
Relay-based auto tuning is a simple way to tune PID controllers
that avoids trial and error, and minimises the possibility
of operating the plant close to the stability limit.

http://homepages.ihug.co.nz/~deblight/AUTResearch/papers/relay_autot.pdf


An Improved Relay Auto Tuning of PID Controllers for SOPTD
Systems


Difficulties of loop tuning
When you discuss loop tuning with instrument and control
engineers, conversation soon turns to the Zeigler-Nichols
(ZN) ultimate oscillation method. Invariably the plant engineer
soon responds with ‘Oh yes, I remember the ZN tuning
scheme, we tried that and the plant oscillated itself into
oblivion — bad strategy. Moreover when it did work, the
responses are overly oscillatory’
So given the tedious and possibly dangerous plant trials
that result in poorly damped responses, it behoves one to
speculate why it is often the only tuning scheme many instrument
engineers are familiar with, or indeed ask if it has
any concrete redeeming features at all.
In fact the ZN tuning scheme, where the controller gain
is experimentally determined to just bring the plant to the
brink of instability is a form of model identification. All
tuning schemes contain a model identification component,
but the more popular ones just streamline and disguise that
part better. The entire tedious procedure of trial and error
is simply to establish the value of the gain that introduces
half a cycle delay when operating under feedback. This is
known as the ultimate gain Ku and is related to the point
where the Nyquist curve of the plant in Fig. 1(b) first cuts
the real axis.

The problem is of course, is that we rarely have the luxury
of the Nyquist curve on the factory floor, hence the
experimentation required.
Abstract Using a single symmetric relay
feedback test, a method is proposed to identify
all the three parameters of a stable second order
plus time delay (SOPTD) model with equal time
constants. The conventional analysis of relay
auto-tune method gives 27% error in the
calculation of ku,. In the present work, a method
is proposed to explain the error in the ku
calculation by incorporating the higher order
harmonics. Three simulation examples are given.
The estimated model parameters are compared
with that of Li et al. [4] method and that of
Thyagarajan and Yu [8] method. The open loop
performance of the identified model is compared
with that of the actual system. The proposed
method gives performances close to that of the
actual system. Simulation results are also given
for a nonlinear bioreactor system. The open loop
performance of the model identified by the
proposed method gives a performance close to
that of the actual system and that of the locally
linearized model. SOPTD model, symmetric relay, auto-tuning

http://ntur.lib.ntu.edu.tw/bitstream/246246/87370/1/09.pdf

DEVELOPMENT OF AN AUTO-TUNING PID AND
APPLICATIONS TO THE PULP AND PAPER INDUSTRY
Abstract
An auto-tuning industrial PID is presented. The autotuning
is realized in three steps. The process is first
adequately excited in order to generate good quality data
for the second step, the process identification. The last step
is the PID tuning based on the evaluated parametric model.
The auto-tuning PID has been implemented on two
different control systems and successful applications to
processes of the pulp and paper industry are analyzed.

http://www.iaeng.org/publication/WCECS2007/WCECS2007_pp175-181.pdf

Auto-tune system using single-run relay feedback test
and model-based controller design
Abstract
In this paper, a systematic approach for auto-tune of PI/PID
controller is proposed. A single run of the relay feedback experiment
is carried out to characterize the dynamics including the type
of damping behavior, the ultimate gain, and ultimate frequency.
Then, according to the estimated damping behavior, the process
is classified into two groups. For each group of processes,
modelbased rules for controller tuning are derived in terms of
ultimate gains and ultimate frequencies. To classify the processes,
the estimation of an apparent deadtime is required. Two artificial
neural networks (ANNs) that characterize this apparent deadtime using
the ATV data are thus included to facilitate this estimation of
this apparent deadtime. The model-based design for this auto-tuning
makes uses of parametric models of FOPDT (i.e. first-order-plus-dead-time)
and of SOPDT (i.e. second-order-plus-dead-time)
dynamics. The results from simulations show that the controllers
thus tuned have satisfactory results compared with those from
other methods.

Tuning strategy for the model-based auto-tune system.


http://w3.gel.ulaval.ca/~desbiens/publications/DevelopmentOfAnAutoTuningPID.pdf

MODIFICATION AND APPLICATION OF AUTOTUNING
PID CONTROLLER
Abstract. This contribution presents a modified autotuning algorithm of the PID controller.
The motivation for the modification of the basic autotuning algorithm is to enlarge the class
of processes to which it can be applied. The basic autotuning algorithm introduced by
Åstrom and Hägglund is extended by the preliminary identification procedure and through
the usage of the dead time compensating controller. These modifications are detailed
through the description of the algorithms’ functioning. The proposed algorithm has been
implemented in the programmable logic controller (PLC) Siemens SIMATIC S7-300. The
experimental results confirm the good robustness properties of the proposed algorithm,
which were demonstrated in a simulation study.

Structure of the modified autotuning PID controller.


http://act.rasip.fer.hr/old/papers/MED00_062.PDF